The curve of an Instalanche
An Instalanche—that’s a link from blogger Glenn Reynolds, who’s otherwise known as Instapundit—can drive a huge amount of traffic to a blog. Glenn’s own blog traffic hovers somewhere in the vicinity of 300,000 hits a day (let me spell that out for you: that’s three hundred thousand). Depending on the time of day, the day of the week, the way Glenn phrases the link, the general interest in the topic, and other variables that remain mysterious, an Instalanche can vary from a modest spike in traffic to a tsunami of visitors.
But I’ve noticed there’s one thing about an Instalanche (or any high-traffic link) that is quite predictable: the graph of the visits always seems to follow a rather strict pattern. There’s a sudden soar the first hour. Then the second hour there’s a fractional step down that represents, very roughly, maybe twenty percent of the whole. Then another similar step down in the third hour, and so on. As the traffic diminishes, the size of the step-downs grows smaller and smaller, and the previously steep imaginary line connecting the steps becomes flatter.
I’m sure there’s a simple equation that expresses the relationship. Here’s a picture of it:
As you can see, this graph charts the number of visitors to my blog yesterday. It is a snapshot taken towards the middle of hour twenty-two. It begins in the wee small hours of the morning, the Sunday after Thanksgiving, ordinarily a very slow time on a very slow day. My traffic was just getting to around the 70 hits-per-hour point when suddenly, at approximately 10 AM, in came the Instalanche and BOOM! went the sitemeter.
There were over 2,400 hits in the first hour after that, about 2,200 in the second, 2,000 in the third, and so on, down to those smaller steps with the smaller decreases between them. This particular Instalanche was good for about 12,500 extra hits that first day—and it’s still going on, albeit at a much reduced rate.
Fun with sitemeters.

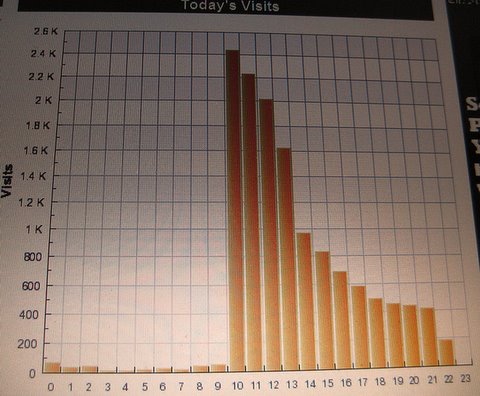
Interesting. Your bar chart looks like a pipe organ.
Exponential decay, or close enough not to matter.
Yeah, rub it in.
Definitely an exponential decay. In fact I calculated the decay constant to be .222/hour and a half-life of about 3.13 hours.
Sorry, couldn’t help myself when presented with such great data. The real question is “Why”.
Physicsguy,
What is the confidence interval for the half-life? #13 an #22 are outliers; not too bad but not right on the curve – at least visually.
physicsguy, I was wondering exactly the same thing: why should the number of hits decay exponentially with time?
Especially since the country comprises four time zones, one would think that the decay would at least be multiphasic.
Even without time zones, I’d have thought that people would hit Instapundit at all times of day, and some fraction of them would then follow the link here, leading to a broad plateau (steady state between people following the link – outflow – versus new people hitting Instapundit – inflow), followed by a drop off (that may be exponential once no new people hit Instapundit).
These data seem more consistent with everyone accessing Instapundit at one time. Curious.
I noticed larger dropoffs in hours 5 and 13. Could that account for the four time zones?
Just as exponential growth describes a function whose derivative with respect to time is dependent on the function’s value at the point in question
dP/dt = a*P(t), “a” a constant,
the solution for which first-order differential equation is
P(t) = e^(a*t)
so for exponential “decay” (far worse than tooth decay!)
dP/dt = -a*P(t) yields
P(t) = e^-(a*t)
Perhaps the exponential falling away of readers is due to diminishing communication among readers, fewer and fewer emailing their friends, as time goes on, to tell each other about Neo’s fantastic post…
😉
To me an even greater mystery is that e^x should be represented by
Σ (x^n)/n!
Jamie Irons
Jamie, the mystery to me is the d/dx (e^x) = e^x. Spooky. You can diffentiate as many times as you like, but each term lopped off at the beginning is replaced by the one following, no matter how fast you differentiate (/g).
We need to get Obama on that, and also on rounding pi down to 3, and e up to 3. That would make life a lot easier.
O.B.,
That is mysterious and wonderful!
Of course, the representation of e^x as an infinite series makes it clear that that “has to happen,” as does the other representation of e^x as
Lim (N->infinity) (1 + x/N)^N
😉
Jamie
Occam’s Beard –
I think many folks use RSS feeds to monitor their sites; by 10, many would have worked through the over-night build up, so the new post would have been indicated on the reader quickly– easily inside of an hour.
Thus, the huge number quickly hitting.
Sort of like a virtual tsunami.
But, the most important (and perhaps hard to measure) are those viewers who come via an instalanche and then bookmark the site and add it to their daily review.
Count me as one of those viewers. Great site.
Foxfier, that makes sense, although I still have some questions re time zones. Ten a.m. EST and 10 a.m. PST are of course three hours apart, so why isn’t the decay multiphasic?
I think you stats doods need to factor in another, well, “factor,” but I’m not sure how to quantify it.Basically, “news junkies” in the day of the new media are like bloodhounds. They are in a rush to find out stuff before it becomes too old to bother with. “Old” is relative, but it is not a very large chunk of the day.
These are the folks who try to get informed fast, spread the word, and move to the next bit of info-prey.
Then there should be a residual group who are merely surfing and reading the news.
Any Ideas how to deal with that in your analysis?
I think it is indicative of the number of people who just look at the first page of the site, the diminishing numbers are the ones that actually scroll down the page to see all of the new links posted since they checked last (like me). Blog dynamics?I saw the link and thought, I already read the best entry on that subject, then I checked the link and smiled, congrats Neo. Thats pretty close to the big time. Way to go.
Here are two simplified models of the world that would lead to exponential decay:
1. Instapundit readers arrive at the site randomly, and once there they read all the posts they have not read yet. As time goes on more and more of the readers are repeat visitors, and they don’t re-read. To take one simple example, suppose there were 100 readers and each had a 50% chance of visiting Instapundit every hour (sounds about right!). In the first hour all 50 visitors would never have seen the link, and all would click. In the next hour, on average only 25 of the 50 would be new to the link. In the next hour, 12.5, and so on…
2. Instapundit readers tend to get distracted as they read down the page. Suppose 100 new readers arrive at the site every hour. They all read the top link, but only 95% of them make it down to the second link. Of those remaining, 95% make it to the third link. Now suppose that a link moves a fixed amount down the page every hour—say 10 slots. Because 0.95^10=0.6 this would mean that in the first hour you’d get 100 hits, in the second hour 60 hits, in the third hour 36…
About the time zones, you’ll notice that this isn’t really exponential decay because the first couple hours don’t decay fast enough. This may be the result of the west coast waking up—essentially, the arrival rate of new visitors would be increasing in the first few hours, counteracting the decay. Also, the 22nd hour might appear to be an outlier if it hadn’t been completed yet when the photo was taken.
Oh, knock it off.
Hey that looks just like a bar graph of my sex life.
Wow. You must have been a very active 10 year old.
Neo, that a couple of your regulars can toss off the basics of the exponential function and its derivatives speaks well of your readership and, I expect, of your blog.
I love the way the mathematicians define e: the limit as n goes to zero of the nth root of ( 1 + n). Identical to Jamie Irons‘s statement, but good for making a jaw drop. (Real mathematicians may be able to explain a difference, unknown to mere mortals, between the two formulations. The invitation is extended.)
I captured an Instalanche sitemeter grab as well, complete with the quantitative hit data. You can see it here.
Jamie, the mystery to me is the d/dx (e^x) = e^x. Spooky. You can diffentiate as many times as you like, but each term lopped off at the beginning is replaced by the one following, no matter how fast you differentiate (/g).
There’s a proof somewhere floating around. Since e is a constant and x is the variable, it is like taking a derivative of A to the x.
Some weird thing with natural logs, however, means that e to the x is its own derivative.
To me an even greater mystery is that e^x should be represented by
Σ (x^n)/n!
Maybe you could blame Taylor for that one.
Pingback:» Thursday Night Links NineCents: The Blog That Makes No Cents
I’ve got an explanation for the whole e^x=Σ (x^n)/n! thing. Bear with me.
The function e^x is the only possible function that is always equal to its own derivative. Its value (for any given x) is always the same as its slope (at that x). Any other function that is equal to its own derivative must be equivalent to e^x.
If you take the derivative of the infinite series
Σ (x^n)/n! = 1 + x/1! + x^2/2! + x^3/3! + …
each term in the series “shifts down” one. The 1 disappears, the x becomes a 1, the x^2/2! becomes x, the x^3/3! becomes x^2/2!, and so on. Because the series is infinite, this means that the derivative is of the series is equal to the series itself. Since it is its own derivative, it must be equal to e^x.